티스토리 뷰
문제
알고리즘
DFS
풀이
포레스트에서 트리의 지배집합의 수를 찾는 문제입니다.
동아리의 홍보효과가 인접한 지역까지 영향을 미칩니다. 하나의 트리에서 문제를 살펴보겠습니다. 잘 생각해보면 리프노드에는 굳이 홍보를 할 이유가 없습니다. 리프노드에 홍보를 하면 자신의 부모노드에만 영향을 미치지만 그 부모노드에 홍보를 하게 되면 리프노드뿐만 아니라 그 부모가 갖는 자식들에게 모두 홍보를 할 수 있기 때문입니다. 즉 리프노드의 부모노드는 무조건 홍보를 해야 이득임을 알 수 있습니다.
[잘못된 풀이]
처음에 이 문제를 리프노드의 부모로부터 BFS를 수행해 현재 노드가 빨간 노드(홍보노드)면 주변은 노 란노드(영향을 받는 노드), 현재 노드가 노란 노드면 주변을 홍보하는 식, 즉 빨간 노드로 만들었습니다. 이 경우는 다음과 같은 반례에 부딪혔습니다.
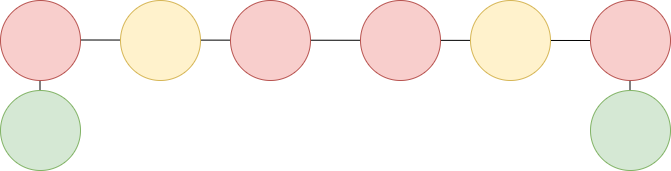
중간에 빨간 노드가 하나만 있으면 되지만 두개가 있는 모습입니다.
[올바른 풀이]
현재 노드의 자식노드들을 검사하여 자식 노드들 중에서 홍보되지 않는 노드가 있다면 현재의 노드를 홍보하는 DFS 풀이를 사용해야합니다. 노드마다 children 배열을 만들어 0에 값이 존재한다면 이는 자식 노드 중 홍보되지 않는 노드가 존재한다는 뜻이므로 현재 노드를 홍보하고 자식노드가 홍보노드(1)라면 현재노드는 영향을 받는 노드(2)입니다. 이 외에는 아무 것도 아닌 노드로 0을 리턴하면 됩니다.
코드
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < n; ++i)
#define REP(i, n) for (int i = 1; i <= n; ++i)
using namespace std;
const int MAXN = 2e5 + 5;
int N, M, ans;
vector<int> adj[MAXN];
bool visited[MAXN];
int dfs(int here) {
visited[here] = true;
int children[3] {};
for (auto there : adj[here]) {
if (!visited[there])
++children[dfs(there)];
}
if (children[0]) {
++ans;
return 1;
}
if (children[1]) {
return 2;
}
return 0;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("in", "r", stdin);
freopen("out", "w", stdout);
#endif
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
cin >> N >> M;
rep(i, M) {
int u, v;
cin >> u >> v;
adj[u].emplace_back(v);
adj[v].emplace_back(u);
}
REP(i, N) {
if (!visited[i] && !dfs(i)) {
++ans;
}
}
cout << ans;
return 0;
}'Algorithm' 카테고리의 다른 글
| [백준 2398] 3인 통화 (0) | 2021.04.24 |
|---|---|
| [백준 4716] 풍선 (0) | 2021.04.15 |
| [백준 1445] 일요일 아침의 데이트 (0) | 2021.04.04 |
| [백준 2276] 물 채우기 (0) | 2021.04.02 |
| [백준 21234] Just Green Enough (2) | 2021.03.31 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- SCC
- dfs
- hld
- sorting
- bfs
- greedy
- Segment tree
- dijkstra
- knapsack
- 이분매칭
- 2-SAT
- union find
- spring boot
- 스위핑
- Suffix Array
- sweeping
- spring
- 정렬
- 이분탐색
- 동적계획법
- 트라이
- 펜윅트리
- DP
- implementation
- 좌표압축
- Oracle
- kmp
- 세그먼트트리
- string
- Fenwick
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
